Addiert man in einem ungekürzten Bruch den Zähler und den Nenner, so erhält man die Zahl 4140. Nach dem Kürzen des Bruches erhält man 7/13.Wie sah der Bruch vor dem Kürzen aus ?
Lösung (von Sophie Müller, Döbeln):
Der ungekürzte Bruch sei a/b. Dann gilt nach Aufgabenstellung
a/b = 7/13 und a + b = 4140. Aus der ersten Beziehung erhalten wir a=7/13·b. Setzen wir diesen Ausdruck für a in die zweite Beziehung ein, so ergibt sich7/13·b + b = 20/13·b = 4140 und daraus schließlich b = 2691 und a = 1449.
Ein Jagdflugzeug flog in einer halben Stunde 200 km weiter als ein Sportflugzeug in einer ganzen Stunde.Wie groß war die Geschwindigkeit jedes der beiden Flugzeuge, wenn die des Jagdflugzeugs dreimal so groß war wie die des Sportflugzeugs ?
Lösung:
Wir ezeichnen die Geschwindigkeit des Jagdflugzeugs (in km/h) mit x und die des Sportflugzeugs mit y. Dann ist x=3*y.
In einer halben Stunde fliegt dann das Jagdflugzeug (x/2) km, das Sportflugzeug in einer ganzen Stunde (y) km. Es gilt alsound wegen x=3*y auch 3/2*y=y+200, weiter y/2=200, somit y=400 und schließlich x=3*y=1200. x/2 = y + 200
Das Jagdflugzeug flog also mit einer Geschwindigkeit von 1200 km/h, das Sportflugzeug mit einer Geschwindigkeit von 400 km/h. Die Probe zeigt, daß das Ergebnis richtig ist.
Gegeben ist ein Dreieck ABC mit rechtem Winkel bei C. Auf der dem Punkt C gegenüberliegenden Seite AB werden zwischen A und B zwei Punkte M und K so markiert, daß l(AC)=l(AM) und l(BC)=l(BK) gilt.Zeige, daß dann w(MCK)=45° gilt !
Dabei bezeichnet l(XY) die Länge der Strecke XY und w(XYZ) die Größe des Winkels mit Scheitel im Punkt Y und Schenkeln XY bzw. YZ.
Lösung:
Seien dei Basiswinkel des rechtwinkligen Dreiecks mit alpha und beta und die drei Winkel mit dem Scheitel C wie folgt bezeichnet:
gamma1=w(ACK), gamma2=w(KCM), gamma3=w(MCB).
Weiterhin sei
alpha1=w(BKC) und beta1=w(AMC).
Für die Basiswinkel der gleichschenkligen Dreiecke KBC und MAC sowie nach dem Außenwinkelsatz gilt dannalpha1 = gamma2 + gamma3 = alpha + gamma1 Addieren wir beide Gleichungen, so erhalten wir
beta1 = gamma1 + gamma2 = beta + gamma3gamma1 + 2*gamma2 + gamma3 = alpha + beta + gamma1 + gamma3 oder2*gamma2 = alpha + beta = 90o, woraus die Behauptung unmittelbar folgt.
Wie viele (echt) fünfstellige Zahlen [abcde] (in dezimaler Schreibweise) haben die Eigenschaft, daß die Summe der ersten beiden Ziffern, die Summe der letzten beiden Ziffern und der Wert der mittleren Ziffer übereinstimmen ?
Lösung von Steffen Biallas (Magdeburg):
Wegen a + b = c = d + e mache ich eine Fallunterscheidung für die Werte a, b, c, d und e, die in Frage kommen:
1. Fall: c=0 ==> keine Lösung, weil a>0 sein muß.
2. Fall: c=1 ==>
| Möglichkeiten für [a;b]: | [1;0] |
| Möglichkeiten für [d;e]: | [1;0], [0;1] |
3. Fall: c=2 ==>
| Möglichkeiten für [a;b]: | [2;0], [1;1] |
| Möglichkeiten für [d;e]: | [2;0], [1;1], [0;2] |
Wenn man dieses Verfahren so weiterführt, erhält man für die folgenden Fälle folgende Möglichkeiten:
4. Fall: c=3 ==> Es gibt 3*4=12 Möglichkeiten.
5. Fall: c=4 ==> Es gibt 4*5=20 Möglichkeiten.
6. Fall: c=5 ==> Es gibt 5*6=30 Möglichkeiten.
7. Fall: c=6 ==> Es gibt 6*7=42 Möglichkeiten.
8. Fall: c=7 ==> Es gibt 7*8=56 Möglichkeiten.
9. Fall: c=8 ==> Es gibt 8*9=72 Möglichkeiten.
10. Fall: c=9 ==> Es gibt 9*10=90 Möglichkeiten.
Als nächstes addiere ich alle Möglichkeiten, und erhalte:
0+2+6+12+20+30+42+56+72+90=330
Es gibt 330 echt fünfstellige Zahlen, die das oben stehende Schema erfüllen.
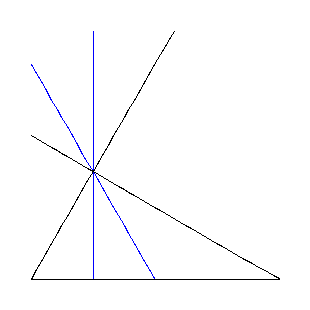
In einem rechtwinkligen Dreieck ABC mit der Hypotenuse AB werde der rechte Winkel durch die Höhe und die Seitenhalbierende durch C in drei gleiche Teile geteilt.Finde heraus, wie viele im wesentlichen verschiedene Dreiecke mit dieser Eigenschaft es gibt, indem Du jeweils die Größe der Innenwinkel angibst. Begründe Dein Ergebnis !
Lösung (von Manuel Mai):

Da der rechte Winkel des Dreiecks ABC (schwarz) durch die beiden Transversalen (blau) in drei gleichgroße Teile geteilt wird, ist jeder der Teilwinkel 30o groß. Da eine der beiden Transversalen die Höhe ist, deren Fußpunkt mit H bezeichnet sei, ergibt sich nach Innenwinkelsatz im Dreieck AHC für den Innenwinkel bei A die Größe 60o und damit verbleiben für den Innenwinkel bei B 30o.
Es gilt folglich bis auf Kongruenz genau ein Dreieck mit der geforderten Eigenschaft. Seine Innenwinkel haben die Größe 30o, 60o und 90o.
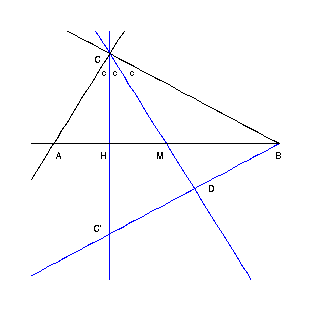
Es sei ein beliebiges Dreieck ABC gegeben, dessen Innenwinkel bei C (wie in Aufgabe 5) durch die Höhe und die Seitenhalbierende durch C in drei gleiche Teile geteilt wird.Zeige, daß ein solches Dreieck immer rechtwinklig sein muß.
Lösung:
Die drei gleichgroßen Teile des Winkels bei C seien (aus technischen Gründen nicht mit dem griechischen Buchstaben Gamma, sondern) mit c bezeichnet. Da CH Höhe und Winkelhalbierende im Dreieck AMC ist, muß dieses Dreieck gleichschenklig sein. HM ist also halb so lang wie AM=BM, d.h. M teilt die Strecke HB im Verhältnis 2:1.
Wir spiegeln nun die ganze Figur an der Geraden AB und erhalten ein (gleichschenkliges) Dreieck BCC'. M ist in diesem Dreieck der Schwerpunkt, denn er teilt die Seitenhalbierende BH im Verhältnis 2:1. Folglich ist CM in diesem Dreieck Seiten- und Winkelhalbierende zugleich, d.h. dieses Dreieck ist auch gleichschenklig mit der Basis BC. Kurz, es ist ein gleichseitiges Dreieck, womit alle Innenwinkel 60° betragen und c=30° folgt.
In dem Schema 43*1*5* ist jede Leerstelle * so mit einer Ziffer auszufüllen, daß die entstehende siebenstellige Zahl durch 75 teilbar ist.Gib an, wieviel siebenstellige Zahlen es insgesamt gibt, die diese Bedingungen erfüllen.
Lösung:
Eine Zahl ist genau dann durch 75 = 3*25 teilbar, wenn sie durch 3 und durch 25 teilbar ist.
Die Teilbarkeit durch 25 kann man an den letzten beiden Ziffern ablesen; die Zahl muß auf 00, 25, 50 oder 75 enden. Die letzte Ziffer der gesuchten Zahl muß also 0 sein.
Eine Zahl ist genau dann durch 3 teilbar, wenn auch ihre Quersumme durch 3 teilbar ist. Diese beträgt 13+x, wenn x die Summe der zwei noch nicht bekannten Ziffern ist. Die Summe der beiden noch fehlenden Ziffern muß also bei Division durch 3 den Rest 2 ergeben. Hierfür gibt es genau die folgenden Varianten:
| Rest 1. Ziffer | Möglichkeiten | Rest 2. Ziffer | Möglichkeiten | |
|---|---|---|---|---|
| 1. Variante: | 1 | 1,4,7 | 1 | 1,4,7 |
| 2. Variante: | 0 | 0,3,6,9 | 2 | 2,5,8 |
| 3. Variante: | 2 | 2,5,8 | 0 | 0,3,6,9 |
Da wir in jeder Zeile jede mögliche erste Ziffer mit jeder möglichen zweiten Ziffer kombinieren können, erhalten wir 3*3+4*3+3*4=33 Lösungen.
Ein Garten von rechteckiger Gestalt ist genau 13 m länger als breit. Um ihn vollständig zu umzäunen, benötigt man genau 92 m Zaun.
- Berechne den Flächeninhalt des Gartens.
- Der Garten soll vollständig in Beete und Wege aufgeteilt werden, wobei folgende Bedingungen zu erfüllen sind:
Untersuche, ob es eine Aufteilung des Gartens gibt, bei der diese Bedingungen erfüllt sind und ermittle ggf. die Anzahl der Beete.
- Jedes Beet hat die Gestalt eines Rechtecks mit den Seitenlängen 3m und 1 m.
- Zwischen je zwei benachbarten Beeten und zwischen dem Zaun und den Beeten ist überall ein 25 cm breiter Weg angelegt.
Lösung:
Für Länge l und Breite b des Gartens gilt 2*(l+b) = 92 und l = b + 13. Daraus ergibt sich l=29,5 Meter und b=16,5 Meter und somit für den Flächeninhalt A=l*b=486,75 m2.
Für Aufgabe b) gilt es, eine Einteilung der Fläche von (29 m)x(16 m) in Beete und Wege zu finden, wobei die Randwege schon abgezogen sind.
Legen wir a Beete mit der Breitseite nebeneinander an, so brauchen wir a-1 Wege zwischen ihnen, was eine Gesamtlänge (in Metern) von a*3+(a-1)*0.25=a*3.25-0.25 ergibt. Für a=9 erhalten wir genau 29 Meter, für a=5 genau 16 Meter.
Legen wir a Beete mit der Längsseite nebeneinander an, so brauchen wir ebenfalls a-1 Wege zwischen ihnen, was diesmal eine Gesamtlänge (in Metern) von a*1+(a-1)*0.25=a*1.25-0.25 ergibt. 29 Meter können wir so nicht auslegen, wohl aber (für a=13) 16 Meter.
Da die Beete längs und breit passen müssen, richten wir sie also mit der breiten Seite in Richtung der 29-Meter-Seite des Gartens aus. Es passen je 13 Beete nebeneinander (zur 16-Meter-Seite) und 9 Beete übereinander (zur 29-Meter-Seite), so daß wir so 117 Beete erhalten.
Kann man allein mit zwei Gefäßen (ohne Maßeinteilung), die genau 9 bzw. 11 Liter fassen, aus einer Wasserleitung eine Portion Wasser von genau 10 Liter abmessen?Lösung:
Fülle das große Gefäß mit 11 l und gieße
davon 9 l in das kleinere Gefäß. Dann verbleiben im großen
Gefäß genau 2 l. Gieße das kleine Gefäß aus
und fülle diese 2 l dorthin um.
Nun fülle das große Gefäß erneut mit 11 l, gieße
daraus das kleine Gefäß voll. Dann verbleiben im großen
Gefäß genau 4 l. Gieße das kleine Gefäß aus
und fülle die 4 l dorthin um.
Nun fülle das große Gefäß erneut mit 11 l, gieße
daraus das kleine Gefäß voll. Dann verbleiben im großen
Gefäß genau 6 l. Gieße das kleine Gefäß aus
und fülle die 6 l dorthin um.
Nun fülle das große Gefäß erneut mit 11 l, gieße
daraus das kleine Gefäß voll. Dann verbleiben im großen
Gefäß genau 8 l. Gieße das kleine Gefäß aus
und fülle die 8 l dorthin um.
Nun fülle zum letzten Mal das große Gefäß erneut
mit 11 l, gieße daraus das kleine Gefäß voll. Dann verbleiben
im großen Gefäß genau 10 l.
Es brennen zwei Kerzen von ungleicher Länge und Dicke. Die längere brennt in 3,5 Stunden herunter, die kürzere (und dickere) in 5 Stunden. Nach zwei Stunden haben die Kerzen gleiche Länge. Um das Wievielfache war die eine anfangs länger als die andere ?Lösung:
Die lange Kerze habe die Länge l, die Kurze die Länge k. Nach
zwei Stunden sind von der langen Kerze noch 1.5/3.5*l, von der kurzen noch
3/5*k übrig, denn die lange Kerze hat noch 1.5 von 3.5 Stunden zu
brennen, die kurze noch 3 von 5 Stunden. Da zu dem Zeitpunkt beide Kerzen
gleichlang sind, gilt
1.5/3.5*l=3/5*k, also l:k=7:5.
a) Untersuche, ob man im Ausdruck 1 o 2 o 3 o 4 o ... o 1999 die o so durch Rechenzeichen + und - ersetzen kann, daß sich als Ergebnis gerade 0 ergibt.Lösung:b) Untersuche dieselbe Frage für den Ausdruck 12 o 22 o 32 o 42 o ... o 19992, der alle Quadratzahlen von 12 bis 19992 enthält.
a) (1+2-3) + (4-5-6+7) + (8-9-10+11) + ... + (1996-1997-1998+1999) = 0
Bei dieser Lösung wird verwendet, daß vier aufeinanderfolgende natürliche Zahlen, mit den Operationszeichen + - - + verknüpft, stets 0 ergeben: Bezeichnen wir die aufeinanderfolgenden Zahlen mit a,a+1,a+2,a+3, so gilt nämlich
b) Ähnlich kann man 8 aufeinanderfolgende Quadratzahlen so addieren bzw. subtrahieren, daß sich gerade 0 ergibt:
Eine Lösung der Aufgabe ist also etwa
Wähle zwei voneinander verschiedene dreistellige Zahlen [abc] und [def]. Bilde daraus die sechsstelligen Zahlen [abcdef] und [defabc] und bestimme deren Differenz. Untersuche, ob diese Differenz durch die Differenz der beiden dreistelligen Zahlen teilbar ist.Lösung (von Steffen Biallas, Magdeburg):a) Gib zwei Beispiele an.
b) Begründe, warum die Division immer aufgeht.
a)
Aus der zweistelligen Zahl 37 machen wir die fünfstellige Zahl 37037. Diese ist durch 91 teilbar.Lösung (von Patrick Reum, Leipzig)a) Gib zwei weitere Beispiele an und untersuche, ob die jeweilige fünfstellige Zahl auch durch 91 teilbar ist.
b) Begründe, warum die Division immer aufgeht.
a) 37037 : 91 = 407, 85085 : 91 = 935
b) Begründung: Die neue Zahl (zb. 37037) entsteht aus der vorgegebenen (zb. 37) durch Multiplikation mit 1001. 1001 ist aber durch 91 teilbar. Aus diesem Grund geht die Division durch 91 auch immer auf.
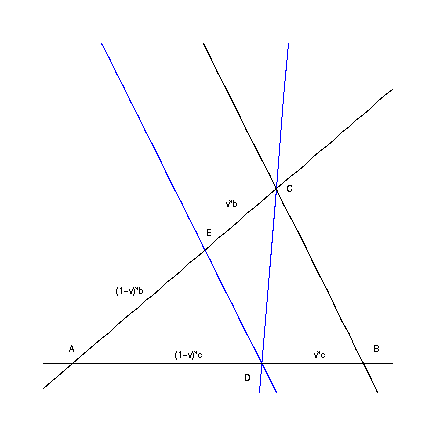
Gegeben sei ein Dreieck ABC und D bzw. E Punkte auf den Dreiecksseiten AB bzw. AC, so daß DE parallel zur Dreiecksseite BC verläuft.a) Sei zunächst DE die Mittellinie, d.h. die Verbindungslinie der beiden Seitenmitten. Bestimme unter dieser Voraussetzung das Verhältnis der Flächeninhalte der Dreiecke CDE und ABC.
b) Sei nun DE eine beliebige Parallele. Welche Werte kann das Verhältnis der Flächeninhalte der Dreiecke CDE und ABC annehmen?
Lösung:
Wir bezeichnen wie üblich die Seitenlängen AB = c und AC = b. Im Aufgabenteil a) liegen D und E genau in der Mitte der Seiten AB und AC, im Aufgabenteil b) teilen Sie die Seiten im gleichen Verhältnis. Wir können also beide Fälle gemeinsam betrachten, wenn wir
AD = (1-v)*c, BD = v*c und AE = (1-v)*b, CE = v*b
setzen (mit v = 1/2 für Teilaufgabe a).Die Dreiecke ADC und ABC haben dieselbe Höhe (aus C). Nach der Flächeninhaltsformel für Dreiecke gilt also
F(ADC)/F(ABC) = (1-v)*c/c = 1-v.
Genauso haben die Dreiecke ADC und CDE dieselbe Höhe (aus D) und es gilt damitF(CDE)/F(ADC) = v*b/b = v.
Zusammen erhalten wirF(CDE)/F(ADC) = v*(1-v).
Sind D und E die Seitenmitten, also v = 1/2, so beträgt das Verhältnis der Flächeninhalte also genau 1:4.
Da
v*(1-v) = v-v2 = 1/4 - (v-1/2)2
gilt (nachrechnen!), kann das Verhältnis der Flächeninhalte für die zulässigen Werte v zwischen 0 und 1 alle Werte zwischen 0 und 1/4 annehmen.Paul und Peter sind begeisterte Jogger und haben sich heute einen "Kanten" von 10 km vorgenommen. Start ist am selben Punkt. Zuerst geht es 5 km bergauf, dann zurück 5 km bergab. Paul bekommt 10 min. Vorsprung, rennt mit 15 km/h bergauf und 20 km/h bergab. Peter rennt mit 16 km/h bergauf und 22 km/h bergab.Lösung von Andreas Klaiber:Wie weit sind die beiden von der Bergspitze entfernt, wenn sie sich begegnen ?
Abkürzungen: s - Weg
t - Zeit
v - Geschwindigkeit
Zur Lösung wird zuerst berechnet, wie lange Paul braucht, um die
Bergspitze zu erreichen:
t = s / v = 5 km / 15km/h = 1/3 h = 20 min
Paul braucht 20 min, um die Spitze zu erreichen.Als nächstes ist herauszubekommen, wie weit Peter derzeit gelaufen ist. Peter rennt 10 min später los als Paul und hat somit nur 10 min (=1/6 h) effektive Laufzeit, die in dieser Rechnung zu beachten sind.
s = v * t = 16 km/h * 10 min = 16 km/h * 1/6 h = 16 km/h /6 h = 8/3 km
Die Entfernung der beiden nach 20 min beträgt demnach5 km - 8/3 km = 7/3 km
Nun läßt sich eine Gleichung aufstellen, mit deren Hilfe die Zeit berechnet werden kann, die bis zum "Treff" noch vergeht:16 km/h * t + 20 km/h * t = 7/3 km.
Die Gleichung besitzt die Lösungt = 7/108 h = 35/9 min.
Nun ist zu sagen, wie weit sie dann von der Spitze entfernt sind:für Paul (bergab): s = v * t = 20 km/h * 7/108 h = 35/27 km
für Peter (bergan): s = v * t = 5 km - 8/3 km - 16 km/h * 7/108 = 35/27 km
Antwort: Sie treffen sich 35/27 km von der Bergspitze entfernt.
Kisten verschiedenen Gewichts sollen transportiert werden. Das Gewicht jeder einzelnen Kiste liegt unter 1 t. Das Gesamtgewicht der Kisten beträgt 10 t. Wieviel 3-Tonner-LKW muß man bestellen, um die Kisten garantiert alle wegzubekommen und keinen der LKW zu überladen?Begründe für Deine Antwort
a) daß man mit der von Dir angegebenen Anzahl LKW die Kisten garantiert abtransportieren kann,
b) daß man mit weniger LKW möglicherweise nicht auskommt.
Lösung:
Vier LKW reichen nicht aus, denn mit ihnen kann man 12 Kisten zu je 0.77 t und eine Kiste zu 0.76 t nicht abtransportieren. Auf jeden 3-Tonner passen höchstens 3 Kisten zu 0.77 t. Also müßte man jeden der 4 LKW auch so beladen und auf keinem bliebe mehr Platz für die kleine Kiste.
Mit fünf LKW kommt man dagegen hin: Lade auf jeden so lange Kisten, bis er mit mindestens 2 t beladen ist.
Einem Schwarm Gänse fliegt eine Gans entgegen und spricht: "Guten Tag, ihr 100 Gänse!". "Wir sind nicht 100 Gänse" antwortet der Führer des Schwarms. "Wenn wir soviel wären wie jetzt und noch einmal soviel und die Hälfte soviel und ein Viertel soviel und dann noch eine Gans, dann wären wir 100 Gänse".Lösung von Steffen Biallas:Wievel Gänse hatte der Schwarm?
Ist x die Anzahl der Gänse, so ergibt sich folgende Gleichung:
2x+x/2+x/4+1=100
Die kann man leicht auflösen und erhält x=36.
In einem Rechteck ABCD sei P ein beliebiger Punkt auf der Diagonalen AC. Die Parallelen durch P zu den Rechteckseiten AB und BC teilen das Rechteck in vier kleinere Rechtecke.Zeige, daß die Rechtecke, in denen P und B bzw. P und D gegenüberliegende Eckpunkte sind, stets gleichen Flächeninhalt haben.
Lösung:
Wir bezeichnen die Seitenlängen des Rechtecks mit |AB|=a und |BC|=b. Weiterhin teile der Punkt P die Diagonale AC im Verhältnis x, d.h. es sei |AP|:|AC|=x und somit |CP|:|AC|=1-x.
Nach Strahlensatz erhalten wir dann für die Längen der Seiten der kleinen Rechtecke x*a und (1-x)*b (Rechteck mit Diagonale PD) bzw. (1-x)*a und x*b (Rechteck mit Diagonale PB).
Daraus folgt unmittelbar die Behauptung: Der Flächeninhalt der kleinen Rechtecke beträgt jeweils x*(1-x)*a*b.
Wir wollen folgende Transformation zweistelliger Zahlen betrachten: Ist [ab] die Zifferndarstellung einer zweistelligen Zahl (im Dezimalsystem), so wird sie durch |a^2-b^2| ersetzt, was wieder eine höchstens zweistellige Zahl ist.Diese Transformation wenden wir so lange an, bis nur noch eine einstellige Zahl übrigbleibt.
Zahlen, für die sich 0 ergibt, nennen wir schnieke.
Fragen / Aufgaben:
- Liste möglichst viele schnieke Zahlen auf !
- Von welchen Zahlen weiß man nach einem einzigen Transformationsschritt, daß sie schnieke sind ?
- Von welchen Zahlen weiß man das nach zwei Schritten ?
- Für welche zweistelligen schnieken Zahlen braucht der Nachweis die meisten Schritte ?
- Erhält man immer nach endlich vielen Transformationen eine einstellige Zahl oder gibt es Teufelskreise ?
- Finde möglichst viele Zahlen, die nicht in einstelligen Zahlen enden ?
- Erstelle ein Diagramm, das das Transformationsverhalten der Zahlen 11 bis 99 veranschaulicht, indem von jeder Zahl zu ihrer transformierten ein Pfeil eingezeichnet ist.
- Aus wievielen Komponenten besteht dieses Diagramm ?
Lösung (von Andreas Klaiber):
1) Schnieke Zahlen (mit Transformationen): 11 --> 0 22 --> 0 29 --> 77 --> 0 33 --> 0 38 --> 77 --> 0 44 --> 0 47 --> 33 --> 0 49 --> 65 --> 11 --> 0 55 --> 0 56 --> 11 --> 0 59 --> 56 --> 11 --> 0 65 --> 11 --> 0 66 --> 0 70 --> 49 --> 65 --> 11 --> 0 74 --> 33 -->0 77 --> 0 83 --> 55 --> 0 88 --> 0 92 --> 77 --> 0 94 --> 65 --> 11 --> 0 95 --> 56 --> 11 --> 0 99 --> 0NB: Das ist eine vollständige Liste aller schnieken Zahlen bis 99, die man mit einiger Geduld und Probieren findet. Man kann sich auch ein kleines Computerprogramm, z.B. für Maple, schreiben, statt selbst zu rechnen:
s:=proc(n) abs(iquo(n,10)^2-irem(n,10)^2) end;
check:=proc(n) local u,m,i; u:=n; m:=n;
for i from 1 to 10 do m:=s(m);
if m<10 then RETURN ([u,m]) else u:=u,m; fi od;
[u]; end;
seq(check(i),i=11..99);
s(n) definiert dabei den Iterationsschritt. iquo und
irem sind ganzzahliger Quotient und Rest bei Division durch 10,
was genau die beiden Ziffern von n liefert. check(n)
erzeugt eine Liste von max. 10 Iterationen, die man sich für alle
Zahlen von 11 bis 99 mit der letzten Zeile ausgeben lassen kann.
Die Übersicht zeigt:
5) Ja, es gibt Teufelskreise, d.h. man kommt nach beliebig vielen endlichen Schritten NICHT zu einer einstelligen Zahl
6) Bsp. für Teufelskreise:
16 -> 35 -> 16 -> 35 etc. 17 -> 48 -> 48 -> 48 etc. 35 -> 16 -> 35 -> 16 etc. 37 -> 40 -> 16 -> 35 -> 16 etc. 40 -> 16 -> 35 -> 16 etc. 48 -> 48 -> 48 etc. 53 -> 16 -> 35 -> 16 etc. 61 -> 35 -> 16 -> 35 etc. 71 -> 48 -> 48 -> 48 etc. 73 -> 40 -> 16 -> 35 -> 16 etc. 84 -> 48 -> 48 -> 48 etc. 89 -> 17 -> 48 -> 48 -> 48 etc. 98 -> 17 -> 48 -> 48 -> 48 etc.
7+8)
0 <- (also schnieke) 22 Zahlen 3 <- 15 Zahlen 4 <- 6 Zahlen 5 <- 6 Zahlen 7 <- 2 Zahlen 8 <- 4 Zahlen 9 <- 21 Zahlen Teufelskreise 16 <-> 35 : 7 Zahlen 48 <-> 48 : 6 Zahlen1, 2 und 6 kommen als Iterationsende überhaupt nicht vor !