Leipziger Schülergesellschaft für Mathematik (LSGM)

Lösungen der Aufgaben des Monats - Schuljahr 2003/04

Aufgabe 1 - Oktober

Anton möchte ein Quadrat in vier deckungsgleiche (kongruente) Teile zerschneiden. Findet möglichst viele Beispiele wie er das tun kann.

Es gibt unendlich viele Möglichkeiten!

Aufgabe 2 - November

a) Es gilt 25 - 15 - 10 = 10 - 6 - 4 also 5 * (5 - 3 - 2) = 2 * (5 - 3 - 2). Deswegen 5 = 2. ? ????

b) Es gilt 1 - 3 + 9/4 = 4 - 6 + 9/4, nach Ausklammern (1 - 3/2) * (1 - 3/2) = (2 - 3/2) * (2 - 3/2). Das heißt (1 - 3/2)² = (2 - 3/2)². Also 1 = 2. ?

c) Findet selbst einen Quatsch-?beweis?! Zum Beispiel für 1 = 10. Oder was Euch sonst so einfällt.

Aufgabe 3 - Dezember

Weihnachtszeit - Bastelzeit! Es geht ums Tangram-Spiel.

Ihr braucht: Karton, Schere oder Cutter, Lineal, Bleistift.

1. Schneidet ein Quadrat zurecht (wählt eine Kantenlänge von etwa 8cm). Markiert ein 4-mal-4-Raster zur Orientierung.

2. Zeichnet die roten Linien ein und schneidet das Quadrat in die sieben Tangramteile.

                               

Und schon kann es los gehen!

a) Ist es möglich....

• ...aus einem Tangramteil ein Quadrat zu legen?
• ...aus zwei der Tangramteile ein Quadrat zu legen?
• ...aus drei der Tangramteile ein Quadrat zu legen?
• ...und aus vieren?
• ...aus fünf?
• ...aus sechs?
• ...und aus den sieben?

Das eigentliche Tangramspiel besteht darin, aus den sieben Teilen vorgegebene Figuren zu legen. Dabei müssen alle Teile benutzt werden, und sie dürfen sich nicht überlappen.

Zum Beispiel kann man folgendes Segelboot legen, nämlich so:

b) Versucht, die folgenden Figuren zu legen:

c) Findet eine schöne Möglichkeit, aus den sieben Teilen eine Kerze zu legen!

a) Ein Quadrat aus 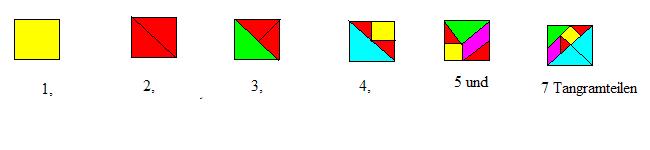Es ist unmöglich, aus sechs Teilen ein Quadrat zusammenzustellen.

b) vier der Figuren: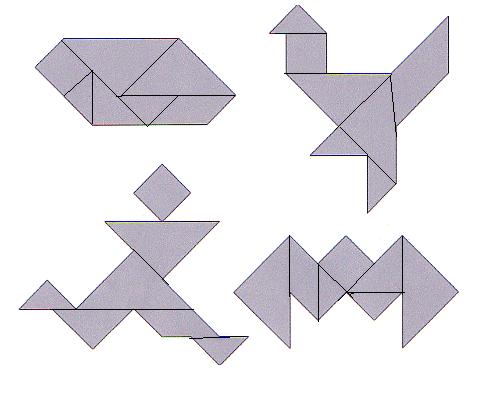

von V. D. Nguyen

von P. Sprenger

von N. Krumbiegel

Aufgabe 4 - Januar

a) Stellt Euch vor, jemand schlägt folgendes Spiel vor:
„Wir werfen zwei Münzen. Bei zweimal Kopf gewinnst du, bei zweimal Zahl gewinnt Micha, und bei einmal Kopf und einmal Zahl gewinne ich.“
Was würdet Ihr davon halten? Sind die Gewinnchancen gerecht verteilt?

Und wie ist es hiermit:
„Wir werfen zwei Würfel. Bei Pasch (= zwei gleiche Zahlen) gibst du mir sechs Stück Schokolade, sonst bekommst du ein Stück von mir.“

b) Stellt Euch vor, Ihr trefft einen Außerirdischen mit drei Armen... Er hat einen Schatz bei sich, den Ihr gewinnen könnt: Er nimmt ihn versteckt in eine seiner Hände, und wenn Ihr auf die richtige tippt, so schenkt er ihn Euch!
Zuerst lässt er Euch eine Hand vermuten. Dann öffnet er eine seiner anderen beiden Hände, und zwar eine leere. Jetzt kommen also nur noch zwei Hände in Frage. Ihr habt nun die Möglichkeit, bei der zuerst gewählten Hand zu bleiben oder Eure Meinung zu ändern, und doch die andere zu nehmen.

Wie würdet ihr entscheiden?

b) Die Wahrscheinlichkeit beim Vermuten, die leere Hand zu wählen, liegt bei 2:3 und die richtige bei 1:3, weil der Außerirdische 3 Hände hat und nur in einer davon der Schatz ist. Der Schatz muss in einer der 3 Hände sein, welche das ist, wissen wir nicht. Beim Vermuten hängt alles noch vom Glück ab, weil man noch gar nichts weiß, aber danach wendet man die folgende Taktik an: Die Wahrscheinlichkeit, eine falsche Hand zu tippen, liegt bei 2:3, also höher als bei einer richtigen, also vermuten wir eine Hand und nehmen an, dass es eine leere ist. Wenn es wirklich eine leere ist, wovon wir ausgehen, dann kann der Außerirdische nur die andere leere Hand öffnen. Und nun, wo nur noch 2 Hände in Frage kommen, ändern wir unsere Meinung und haben den Schatz gewonnen, weil wir von der leeren Hand auf die richtige wechseln.

Diese Taktik geht aber nur, wenn man am Anfang eine leere Hand vermutet, denn wenn man eine richtige vermutet, dann hat der Außerirdische 2 leere Hände zur Auswahl und öffnet eine davon. Wenn man seine Meinung jetzt ändert, dann hat man eine leere Hand getippt.

Die Wahrscheinlichkeit, mit der oben aufgelisteten Taktik zu gewinnen, liegt bei 2:3, denn Glückssache ist nur das Vermuten, und die Wahrscheinlichkeit, dass man die leere Hand vermutet, ist 2:3, der Rest ist kein Glück, sondern Taktik, wie oben gezeigt. Wenn man aber am Anfang eine richtige Hand vermutet, dann sind die Gewinnchancen 1:3, weil die Wahrscheinlichkeit eine richtige Hand zu vermuten bei 1:3 liegt und außerdem die Taktik nicht funktioniert.

Somit gibt es keine Strategie, mit der man zu 100% gewinnt, aber eine, wo man eine Gewinnchance von 2:3 hat.

Aufgabe 5 - Februar

Wieder etwas zum Basteln! Ihr braucht: Papier, Schere, Kleber, Lineal, Stift. Schneidet einen Papierstreifen zurecht:

Schreibt darauf den folgenden Text ; -)

Klebt den Steifen zu einem Band, indem ihr die schraffierten Stellen aufeinander klebt (so dass die beiden A's aufeinander zu liegen kommen). Dazu müsst ihr das Band einmal in sich verdrehen. Das muss dann etwa so aussehen:

a) Was ist nun aus dem Text geworden? Wie ist das passiert?
Ein solches verdrilltes Band nennt man übrigens Möbiusband (nach dem Mathematiker August Ferdinand Möbius). Es hat viele merkwürdige Eigenschaften. Zum Beispiel hat es bloß eine Seite! Stellt Euch vor, eine Ameise krabbelt auf dem Band Längsrichtung. Wo ist sie nach 20 cm angekommen, wo nach 40 cm?
Durch wie viele Kanten wird das Möbiusband begrenzt?

b) Ein Zauberer kommt mit drei langen Papierbändern auf die Bühne. Eines ist rot, eines blau und das dritte ist gelb. Man kann nicht erkennen, ob sie verdreht sind oder nicht. Er schneidet jedes der Länge nach auf:

         

Beim roten Band erhält er zwei ineinanderhängende Bänder. Beim blauen Band erhält er zwei einzelne Bänder. Beim gelben Band erhält er ein einziges, ganz langes Band.

Welches der Bänder könnte ein Möbiusband gewesen sein? Und die anderen beiden Bänder, waren sie wohl verdreht, und wenn ja, wie oft? Wie oft verdreht sind die Bänder, die der Zauberer nach dem Schneiden erhalten hat?
Um das herauszukriegen, bastelt Ihr am besten noch ein paar Möbius- und andere Bänder und probiert aus. Schneidet auch noch die Ergebnisse auf!
Viel Spaß, und nicht die Nerven verlieren!

c) Wettbewerb
Wer schreibt den besten Text mit "Möbius"-Effekt (so wie im Beispiel mit der Schule)? 

von P. Sprenger (Gewinner des Wettbewerbs)

Matheunterricht ohne Taschenrechner, das ist
was ich brauche
Ich habe Freude am Denken

Stillos
ist eine Lösung
wenn der Computer es tut

Dies ergibt nach Zusammenkleben des Möbiusbandes:

Matheunterricht ohne Taschenrechner, das ist stillos.
Was ich brauche ist eine Lösung.
Ich habe Freude am Denken, wenn der Computer es tut.

von N. Krumbiegel

Im Winter
ist es total blöd
nicht in die Schule zu können

wenn es schneit und weht,
doch in die Schule zu kommen,
das ist super!

von O. Medvedyev

Ich mag
das Nichtstun
Ich freue mich auf
die Tage des Nichtstuns

Die Aufgabe des Monats zu lösen,
ist eine Qual.
Die Ferien
kommen bald.

Aufgabe 6 - März

a) Ihr seid auf Abenteuerreise und kommt an eine Weggabelung. Ihr wisst, dass ein Weg nach Indien führt, der andere aber bloß nach Erfurt. Ihr wollt natürlich nach Indien!
Die Gabelung wird von zwei Menschen bewacht, von denen einer immer lügt, und der andere immer die Wahrheit sagt, aber Ihr wisst nicht, wer der Lügner und wer der Ehrliche ist.
Ihr könnt einem von ihnen eine Frage stellen, um zu erfahren, welcher der richtige Weg ist.

Was würdet Ihr fragen?

b) Ihr habt den richtigen Weg gefunden, und kommt auf eine Insel, die von Lügnern und Ehrlichen bewohnt wird. Insgesamt sind es hundert Einwohner. Ihr seid neugierig, und fragt jeden einzelnen, wieviele Lügner es denn auf der Insel gebe. Der erste, den Ihr fragt, antwortet: es gibt mindestens einen. Der zweite antwortet: es gibt mindestens zwei, der dritte: mindestens drei, usw. Der hundertste sagt: es gibt mindestens hundert.

Wieviele Lügner leben auf der Insel?

c) Ihr kommt auf eine andere Insel, die 15 Einwohner hat. 10 von ihnen sind ehrlich, die anderen 5 sagen manchmal die Wahrheit, und manchmal lügen sie. Ihr sollt heraus bekommen, wer die Ehrlichen sind. Dazu könnt Ihr so viele Fragen stellen, wie ihr wollt. Wie geht das?

Seien es nun bloß 5 Ehrliche unter den 15. Zeigt, dass Ihr eventuell (das heißt, wenn die Gelegenheitslügner es so wollen) überhaupt nichts darüber erfahren könnt, wer ehrlich ist.

Wenn es hingegen 4 Ehrliche sind, werdet Ihr bei manchen Einwohnern entscheiden können, ob sie zu den Ehrlichen gehören oder nicht. Bei mindestens wievielen Einwohnern?

Allgemein: Wenn es n Einwohner sind, davon k Ehrliche, über wieviele Einwohner mindestens wird man etwas aussagen können?

Lösung der Teile a) und b) von P. Sprenger:

a) Man muss fragen: Welchen Weg würde mich der andere nach Indien schicken?
Denn der Lügner würde mir immer den falschen Weg zeigen. Der, der die Wahrheit sagt, auch. Man muss dann also den anderen Weg wählen.

b) Es gibt 50 Lügner und 50 Ehrliche. Die zuerst befragten Personen (1 bis 50 ) sagen die Wahrheit.

Lösung des Teils c) :

Man fragt jeden, wer immer ehrlich sei. Alle 10 Ehrliche geben die gleichen Personen an. Die anderen 5 können sagen, was sie wollen -- die Ehrlichen sind jedenfalls genau die sind, die mindestens 10mal gemeinsam genannt worden sind.
Das funktioniert immer, solange die Ehrlichen in der Überzahl sind. Aber auch, wenn es 4 Ehrliche unter den 15 gibt, kann man etwas rausbekommen: denn sobald jemand nicht sich selbst als Ehrlichen nennt, ist klar, dass er nicht zu den Ehrlichen gehört. Außerdem muss die Gruppe der Ehrlichen mindestens 4mal genannt werden. Die Unehrlichen können einem also bloß etwas vormachen, indem sie sich in Vierergruppen gegenseitig nennen. Dann bleiben aber 3 Einwohner übrig, die dann als unehrlich überführt sind.

Wenn es allerdings 5 Ehrliche unter den 15 gibt, dann können sich die 10 Unehrlichen in zwei Fünfergruppen teilen, und jeder tut so, als sei gerade seine Gruppe die Gruppe der Ehrlichen. Man kann nichts herausbekommen!

Allgemein: Bei n Einwohnern und k Ehrlichen kann man mindesten über so viele Personen aussagen, dass sie unehrlich sind, wie bei der Aufteilung der n Einwohner in Gruppen von k Personen übrigbleiben. Das ist gerade der Rest von n bei Teilung durch k ( = n mod k, für diejenigen, die den Modulus schon kennen).

Aufgabe 7 - April

Aufgabenstellung:

Viel Spaß!
Für a) und b) braucht Ihr eine passende Schnur, nicht zu kurz. Paketschnur ist gut geeignet.
einfacher Knoten

a) Wer schafft es, mit nur einer Hand eine Schnur zu knoten (in der Luft, und ohne den Mund oder so zu benutzen)?
Und wie kriegt man es hin, ohne den Daumen zu benutzen? Startet wie auf dem Bild zu sehen, und lasst den Knoten dann sozusagen auf die Schnur fallen (Ihr braucht ihn nicht festzuziehen).

b) Jetzt mit beiden Händen. Aber!
Legt die Schnur glatt vor Euch hin. Nehmt die Schnur auf - ein Ende in die linke Hand, das andere in die rechte. Und nun dürft Ihr nicht mehr loslassen. Bekommt Ihr einen Knoten in die Schnur?
Versucht es zunächst, ohne die Denkanstöße zu lesen.
Ein erster Tipp: Denkt nach, bevor Ihr die Schnur in die Hände nehmt.
Und: Es geht.

c) Zusatz 
Dieser Aal namens Myxine kann seinen eigenen Körper knoten!
Findet etwas über ihn heraus, und beschreibt, wie er diese Fähigkeit nutzt.

Denkanstöße zu b)

1. Wieso nennt man A einen Knoten und B nicht?

A

B

     

2. Weil, wenn man die Schnur in die Hände nimmt, und zieht...

3. Mathematischer ausgedrückt, lautet die Frage "Knoten oder nicht?" wie folgt:
Schliesst man die Schnur, ist sie dann in einen glatten Ring wie A verformbar? Ohne die Schnur zu zerschneiden natürlich!
Wenn nicht, dann ist es ein Knoten. Welche der folgenden Figuren sind Knoten?

A

B

C

D

E

F

4. Was hat das mit der Aufgabe b) zu tun ("Schließt man die Schnur...")?

5. Ist es also unmöglich?

6. Wer schließt wen?

Aufgabe 8 - Mai

a) Was bedeuten diese Nachrichten?

1.

2.

3.

4.
5.

b) Zusatz
Denkt Euch eine Geheimschrift aus, und sendet eine Botschaft zum Entschlüsseln. 

Lösungen:

1) RJK 

2) BEN LIEBT KARIN

3) morgen um fünf am hafen

4) SAG_DEN_ANDERN_BESCHEID

5) DER_SCHATZ_IST_IN_DER_GROTTW 

Ich bitte um Entschuldigung für die Mal- und Schreibfehler in 1) und 5); in 1) sollte eigentlich "OK!" herauskommen, und der Schatz ist natürlich in der Grotte.

1) von B. T. Thanh:

5/4/15/3

2) von N. Krumbiegel:

         !
+      ! !
+    ! / ?
+  ? & % ?
----------
   ! $ / /

1=W 2=T 3=H 4=N 5=I 6=L 7=E 8=R 9=S 0=O

3) von V. D. Nguyen

Code: 1661 (Römer)                            

Hinweis: G=Z M=G D=E Z=U C=H L=E Q=? X=I I=M Y=A S=O 

-> Lösungen

Aufgabe 9 - Juni

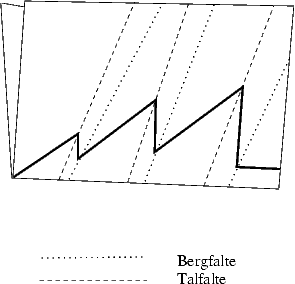
a) Nehmt Euch ein quadratisches Blatt Papier und faltet es zu einem Viertel zusammen. Fahrt fort, wie auf den Bildern zu sehen. Am Schluss schneidet Ihr entlang der blauen Linie.Was erhaltet Ihr, wenn Ihr das hier blau gekennzeichnete Stück wieder auseinander faltet?

Die Aufgaben bestehen nun alle darin:
Man faltet ein Blatt Papier auf eine bestimmte Weise, macht einen einzigen geraden Schnitt, und erhält eine schöne Figur.

Was für Figuren sind wohl möglich? Sie sind natürlich immer durch gerade Linien begrenzt.

b) Schafft Ihr es,

• einen fünfzackigen Stern
• einen Tannenbaum
• einen Fisch
• Euren Anfangsbuchstaben

zu erhalten?
Bei Fisch und Buchstabe sind "eckige" Versionen gemeint, klar.
Tipp: Zeichnet in etwa vor, was Ihr erhalten wollt, und versucht dann, die entsprechende Faltung zu finden. Wenn es zu schwierig ist, vereinfacht lieber die Form, bevor Ihr verzweifelt!

c) Versucht, ein möglichst lustiges Gesicht zu erhalten.

Hinweis: In der ZEIT erschien ein lesenswerter Artikel ( http://www.zeit.de/2004/06/P-Origami) über den Wissenschaftler, welcher bewiesen hat, dass man tatsächlich alle durch gerade Strecken begrenzte Figuren auf diese Weise erhalten kann. Er ist erst 22 Jahre alt! Ihr erfahrt auch, warum solche Fragen nicht nur theoretisch von Interesse sind, und was es sonst noch für Origami-Probleme gibt.

Lösungen:

a) Man erhält einen sechseckigen Stern, aus dem ein kleinerer sechseckiger Stern herausgeschnitten ist.

b) Tannenbaum

einfache Variante (von O.Medvedyev):

Um einen Tannenbaum zu bekommen, nimmt man ein quadratisches Blatt Papier und faltet es so, dass 2 gleiche rechteckige Hälften entstehen. Dann schneidet man das zusammengefaltete Blatt Papier diagonal durch und hat einen Tannenbaum: ein gleichschenkliges Dreieck.

kompliziertere Variante:

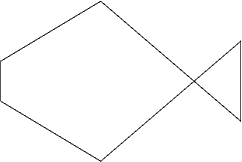
• Fisch (von O.Medvedyev)

Man nimmt wieder ein quadratisches Blatt Papier und faltet es in 2 gleiche Teile zusammen, sodass 2 gleiche rechteckige Hälften entstehen. Dann nimmt man eine Seite des Rechtecks und faltet sie so, dass sie mehr als die Hälfte der Fläache einnnimmt und den übriggebliebenen Rest faltet man auch so, dass er mit der anderen Seite in Berührung kommt, aber sie dürfen sich nicht überschneiden. Das Papierstück ist jetzt 4-lagig. Dann schneidet man das Blatt Papier diagonal durch und wenn man es auseinander faltet, hat man einen Fisch.

Bemerkung: wenn man nicht genau diagonal schneidet, sondern ein bißchen versetzt, bleibt auch der Fischschwanz dran.

Aufgabe 10 - Sommeraufgabe

Ich habe alle Hände voll zu thun, ich weiß mir vor Arbeit nicht zu helfen.
Sehen Sie, erst habe ich auf den Stein hier dreihundert fünf und sechzig Mal hintereinander zu spucken. [...]
Dann - sehen Sie diese Hand voll Sand?
(Er nimmt Sand auf, wirft ihn in die Höhe und fängt ihn mit dem Rücken der Hand wieder auf.)
jetzt werf' ich sie in die Höhe. Wollen wir wetten?
Wieviel Körnchen hab' ich jetzt auf dem Handrücken?
Grad oder ungrad?

aus: Leonce und Lena von Georg Büchner

Diesmal geht es um Zahlen: große und kleine und mittlere. Auf die meisten Fragen gibt es keine genaue Antwort - auf die kommt es auch nicht so sehr an, sondern darauf, wie Ihr sie herausbekommt!
Dazu braucht Ihr Hilfsmittel - ein Maßband gewiss, ein Lexikon, vielleicht eine Stoppuhr, und auch Hilfe (Euer Apotheker hat eine genaue Waage, Eure Geschwister sind bestimmt gut in Physik, u.s.w. ...). Es geht nicht darum, alles zu bearbeiten, sondern darum, sich originelle Experimente auszudenken und, soweit möglich, durchzuführen. Ihr könnt auch versuchen, zu einer Frage ganz viele verschiedene Lösungswege zu finden. Und bestimmt gibt es Freiwillige für einen Schätzwettbewerb.

Los geht's!

• Wieviele Sandkörner kannst du in deiner Hand halten?
• Wieviel Gramm Salz sind in einem Glas Meerwasser?
• Wie weit ist der Mond von der Erde entfernt?
• Wieviel Luft ist in Deinem Zimmer?
• Wie lange dauert ein Moment?
  
• Wie alt sind die Bäume in deiner Strasse?
• Wieviele Kilometer haben diese Aufgaben bis zu deinem Rechner im Internet zurückgelegt?
• Wieviele Kinder in deinem Alter leben auf der Erde?
• Wieviel Volumen Loch ist in einem Schweizer Käse?
• Wie hoch ist das Haus, in dem du wohnst?
• Wieviele Beine hat ein Tausendfüßer?
• Wie lange reist ein Wassertropfen vom Meer bis er als Regen fällt?
• In wievielen Sprachen kannst du "Hallo" oder "Guten Tag" sagen?
• Wie dünn ist ein Haar?
• Wieviele Sterne stehen am Himmel?
  

Lösungen:

N. Krumbiegel schreibt:
Das ist abhängig von der Größe der Sandkörner und ob sie nass oder trocken sind. Ich habe es mit trockenem Sand von der Ostsee versucht. Zuerst habe ich den Sand, den ich in der Hand halten kann, gewogen und dann eine kleinere Anzahl gezählt und gewogen. So habe ich herausgefunden, dass man ca. 1520000 Sandkörner in der Hand halten kann.

V. D. Nguyen hat es etwas vereinfacht und Kiesel genommen:

Gesamtmasse in der Hand: 20,49g  
Ein Kiesel: 0,07g
Berechnung: 20,49g/ 0,07g= 292, also ca. 300 Kiesel

Wieviel Gramm Salz sind in einem Glas Meerwasser?

N. Krumbiegel schreibt:
Ein Glas Ostseewasser 0,3l enthält 3g Salz; dieses Ergebnis erhält man, wenn man das Wasser verdunsten lässt.

Eine anderes Experiment, nach einer Idee von V. D. Nguyen:
Zuerst nimmt man ein Glas reines Wasser, fügt Salz hinzu, und versucht herauszufinden, ob und wie sich das Volumen ändert - wieviel Volumen pro Gramm Salz hinzu kommt. Dann wiegt man ein Glas Meerwasser (das schwerer ist als ein Glas reinen Wassers), und berechnet per Gleichungssystem die Salzmenge.

O.Medvedyev hat gelesen:
Die durchschnittliche Salzkonzentration im Meerwasser beträgt etwa 2%. In ein Glas passen 200ml, das sind ca. 200g Meerwasser, also rechnet man 200g * 0,02 = 4g. Ein Glas Meerwasser enthält etwa 4g Salz. Aber im Toten Meer ist die Salzkonzentration im Wasser 27%, sodass in einem Glas mit dem Wasser aus dem Toten Meer 200g*0,27=54g Salz sind. Solche Eigenschaften hat auch ein Golf im Kaspischen Meer und der See Elton, die beide eine Salzkonzentration von 27% haben.

Wie weit ist der Mond von der Erde entfernt?

O.Medvedyev hat es ausgemessen:
Ich habe mit dem Jakobstab gemessen unter welchem Winkel man den Mond sieht und habe 0,5° rausbekommen. Weiterhin muss man rausbekommen, was diese 0,5° überhaupt bedeuten. Wie weit muss ein Gegenstand vom Beobachter entfernt sein, um ihn unter dem Winkel von 1° zu sehen? Mit anderen Worten müssen wir den Radius des Kreises, in dessen Mitte wir stehen, ausrechen, wobei am Kreisrand ein Gegenstand sich befindet mit der Größe 1 LE, der unter dem Winkel von 1° zu sehen ist. Wenn der Gegenstand mit der Größe 1 LE unter dem Winkel 1° zu sehen ist, dann beträgt der Kreis mit dem Vollwinkel 360° auch 360 LE. Der Radius ist 2 pi kleiner als der Kreis, also betraägt er: 360 LE/(2 pi) = 57,3 LE, also etwa 57 LE. D.h., wenn die Entfernung zwischen Gegenstand und Beobachter 57 mal größer ist als der Gegenstand, dann ist der Gegenstand unter einem Winkel von 1° zu sehen. Da der Mond aber nur unter dem Winkel 0,5° von der Erde zu sehen ist, ist er von der Erde 57*2 = 114 Monddurchmesser entfernt. Der Monddurchmesser beträgt etwa 3330 km, also beträgt die Entfernung Mond-Erde 3330 km*114 = 379.620 km, also rund 380.000 km.

Im Lexikon steht: Die Entfernung schwankt zwischen 363 300 km und 405 000 km, die mittlere Entfernung beträgt 384 400 km.

Wie lange dauert ein Moment?

O.Medvedyev meint:
Ein Moment ist das Blinzeln mit den Augen. Das dauert 2/5 s und wird in folgende Phasen unterteilt: Zuklappen der Augenlider (75-90/1000s), Augenlider im geschlossenen Zustand (130-170/1000s) und Aufmachen der Augenlider (170/1000s).

Wieviele Kinder in deinem Alter leben auf der Erde?

V. D. Nguyen schlägt vor:
Ich bin 13 Jahre alt. Ich könnte es so machen, dass jeder, der 13 Jahre ist, auf einen großen Platz kommen soll und wenn alle da sind, zähle ich die ganzen Kinder. Wäre ich sehr reich, müssten die Kinder nichts bezahlen (z. B. Flugticket...).

In wievielen Sprachen kannst du "Hallo" oder "Guten Tag" sagen?

Zusammen kommen wir auf über 20!
Deutsch: Hallo - Französisch: Bonjour / Salut - Englisch: Hello - Vietnamesisch: Sin chao - Chinesisch: ,,Nihao “ (so ähnlich gesprochen) - Spanisch: Buenos dias! - Ungarisch: Jo napot kivanok! - Griechisch: Kalimera sas! - Türkisch: Merhaba! - Japanisch: Ohayoh! - Kroatisch: Dobar dan! - Tschechisch: Dobry den! - Polnisch: Dzien dobry / cze´s´c! - Litauisch: Laba diena! - Finnisch: Päivä! - Russisch: Privet/ Dobrij den - Ukrainisch: Vitaju! - Latein: Ave, Salvete - Italienisch: Buon giorno, ciao - Portugiesisch: Bom dia/ Olà - Hebräisch: Shalom - Arabisch: A s-salamu alaykum!

Lösungen der Schülervorschläge

Aufgabe 3, Tangramkerzen:

von V. D. Nguyen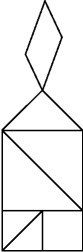

von P. Sprenger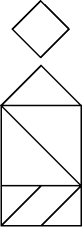

von N. Krumbiegel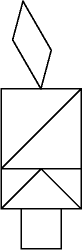

Aufgabe 8, Geheimschriften:

1) Code
2) TOLL
3) 1661 = römische Zahl bilden, die wie Buchstaben aussehen = MDCLXI     M = G ; D = E; C = H; L = E; X = I; I = M   = GEHEIM

LSGM	$Id: loesungen.html,v 1.14 2004/09/08 11:33:55 graebe Exp $