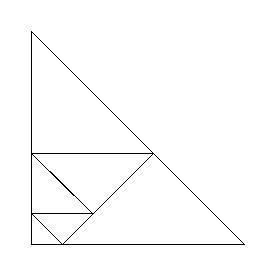
 | Dass die Dreiecke alle unterschiedliche Größe haben, erkennt man am besten, wenn man sich die ganze Figur auf Kästchenpapier aufzeichnet (wobei das kleinste Dreieck genau ein halbes Kästchen ausfüllt). |
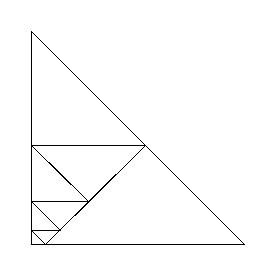
Und hier noch eine zweite Lösung:
| Aufgabe | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|
Anja, Bärbel, Chris und Doris erzählen vom 60-m-Lauf:Anja: Ich war weder Erste noch Letzte.Es stellte sich heraus, daß genau eines der Mädchen nicht die Wahrheit gesagt hatte. Wer? Und wie lautete der Einlauf ?
Bärbel: Ich war nicht Letzte.
Chris: Ich war Erste.
Doris: Ich war Letzte.
Lösung (von Carolin Schwarz, Leipzig):
Hätte Anja gelogen, so wäre sie 1. oder 4. geworden. Wäre sie 1., so hätte auch Chris gelogen. Wäre sie 4., so hätte auch Doris gelogen. Also muss Anja die Wahrheit gesagt haben.
Hätte Bärbel gelogen, so müsste auch Doris gelogen haben. Also muss auch Bärbel die Wahrheit gesagt haben.
Hätte Doris gelogen, so wäre keines der Mädchen Letzte geworden. Also muss auch Doris die Wahrheit gesagt haben.
Folglich hat Chris gelogen, Doris war 4. und Bärbel 1. Über die Vergabe der beiden anderen Plätze kann aus den gegebenen Aussagen keine eindeutige Schlußfolgerung abgeleitet werden.
Untersuche, ob man ein gleichschenklig-rechtwinkliges Dreieck in kleinere gleichschenklig-rechtwinklige Dreiecke zerlegen kann, die noch dazu paarweise unterschiedliche Größe haben!
Lösung (von Carolin Schwarz, Leipzig):

Dass die Dreiecke alle unterschiedliche Größe haben, erkennt man am besten, wenn man sich die ganze Figur auf Kästchenpapier aufzeichnet (wobei das kleinste Dreieck genau ein halbes Kästchen ausfüllt). Und hier noch eine zweite Lösung:
Unter dem Zeichen n! (gelesen n Fakultät) versteht man das Produkt der ersten n natürlichen Zahlen, also z.B.10! = 1*2*3*4*5*6*7*8*9*10 = 3628800 Ermittle, wie oft man 1000! durch 1001 teilen kann.
Lösung:
Es war zu bestimmen, wie oft man 1000! durch 1001 (natürlich ohne dass ein Rest bleibt) teilen kann. Da 1001=7*11*13 gilt, müssen wir dazu ermitteln, wie oft die Primfaktoren 7, 11 und 13 in der Primfaktorzerlegung von 1000! auftreten.Wir untersuchen das exemplarisch für die Zahl 7: Da 1000! das Produkt aller Zahlen von 1 bis 1000 ist, brauchen wir nur das Vorkommen des Faktors 7 in den Faktorzerlegungen der einzelnen Faktoren zu addieren. In den Zahlen 7, 14, 21, ..., 994 kommt der Faktor 7 vor (142 Zahlen); in den Zahlen 49, 98, ..., 980 kommt der Faktor 7 ein zweites Mal vor (20 Zahlen); in den Zahlen 343 und 686 sogar ein drittes Mal (2 Zahlen). Zusammen ergibt das 142+20+2=164 Faktoren 7 in der Faktorzerlegung von 1000!.
Genauso erhält man 90+8=98 Faktoren 11 und 76+5=81 Faktoren 13. Da man für einen Faktor 1001 jeden der drei Primfaktoren genau einmal braucht, kann man demzufolge 1000! genau 81 mal durch 1001 teilen.
Gegeben seien drei Punkte der Ebene, die nicht auf einer Geraden liegen.Lösung (nach Manuel Mai, Leipzig):Untersuche, ob es eine oder mehrere Geraden gibt, die von allen drei Punkten den gleichen Abstand haben.
Wieviele solche Geraden gibt es und wie kann man deren Lage beschreiben?
Was kannst Du noch über diese Geraden aussagen?
Ja, gibt es:
Es gibt 3 solche Geraden. Da jede Gerade durch den Mittelpunkt einer Strecke von deren Endpunkten gleichweit entfernt ist, muss jede von drei vorgegebenen Punkten gleichweit entfernte Gerade durch die Mitten von zwei der Verbindungsstrecken (und damit parallel zur dritten Verbindungsstrecke) verlaufen.
Die gesuchten Geraden sind also genau die Mittellinien im Dreieck, das durch die drei gegebenen Punkte gebildet wird.
Ein Holzrahmen in Form eines gleichseitigen Dreiecks liegt auf einem Tisch. Im ihm sind Tischtennisbälle so dicht wie möglich gepackt. Genau sechs Bälle passen an einer Holzkante nebeneinander. Auf dieser ersten Schicht liegt eine zweite Schicht von Tischtennisbällen, jeder von ihnen in der Lücke, die drei sich gegenseitig berührende Bälle der ersten Ebene bilden. Und so geht es weiter, Schicht für Schicht, bis ganz oben, wo als sechste Schicht noch ein einzelner Ball liegt.1. Gib an, wieviele Tischtennisbälle sich insgesamt in der Pyramide befinden. (3 Pkt.)
2. Wieviel Tischtennisbälle braucht man für eine (rekordverdächtige) solche Pyramide mit hundert Etagen? (5 Pkt.)
Lösung:
1. (von Carolin Schwarz, Leipzig): Es befinden sich insgesamt 56 Bälle in der Pyramide.In der untersten Schicht befinden sich 21 Bälle (=6+5+4+3+2+1), darüber ("auf Lücke") noch 15 (=5+4+3+2+1), in der dritten Schicht noch 10 (=4+3+2+1) und weiter 6, 3, 1 Bälle. Zusammen sind das 21+15+10+6+3+1=56 Bälle.
2. Genauso können wir für eine Pyramide mit 100 Etagen argumentieren: In der obersten Schicht liegt 1 Ball, in der zweiten (von oben) 1+2 Bälle, in der dritten 1+2+3 Bälle usw. Zählen wir die Summen clever zusammen (100 Summanden 1, 99 Summanden 2 usw.), so erhalten wir nach fleißigem Rechnen
100*1 + 99*2 + 98*3 + ... + 2*99 + 1*100 = 171700 Bälle
NB: Für eine Pyramide mit n Reihen erhält man auf diesem Weg als Zahl der Bälle
sum(i*(n+1-i),i=1..n) = 1/6 * n * (n + 2) * (n + 1)
Ein Holzwürfel mit grüngefärbter Oberfläche wird in 27 gleichgroße Teilwürfel zersägt.1. Wie viele der Teilwürfel haben 0, 1, 2, 3, 4, 5 bzw. 6 grüne Seitenflächen ?
2. Überlege (und begründe), wie die Antwort bei 1 000 000 gleichgroßen Teilwürfeln lautet.
Lösung (von Eva Perlt, Leipzig):
1. 0 grüne Seitenflächen hat genau ein Würfel. Er befindet sich im Inneren des "Ursprungswürfels" und hat somit keinen Anteil an dessen Oberfläche, die grün gestrichen wurde.1 grüne Seitenfläche haben genau 6 Würfel. Diese befinden sich in den Mitten der 6 Seitenflächen des "Ursprungswürfels".
2 grüne Seitenfläche haben genau 12 Würfel. Diese befinden sich in den Mitten der 12 Kanten des "Ursprungswürfels".
3 grüne Seitenfläche haben genau die 8 Würfel, die sich an den Ecken des "Ursprungswürfels" befinden.
Es gibt keine Würfel mit mehr als 3 grünen Seitenflächen.
2. Wird der "Ursprungswürfel" in 1000000 Teilwürfel zersägt, so wird dabei jede seiner Kanten in 100 Teile geteilt. Wie oben erhält man dabei
- keine Würfel mit mehr als 3 grünen Seitenflächen,
- an den Ecken 8 Würfel mit 3 grünen Seitenflächen,
- längs der Kanten 12*(100-2)=1176 Würfel mit 2 grünen Seitenflächen,
- im Inneren der Seitenflächen 6*(100-2)2=57624 Würfel mit 1 grünen Seitenfläche und
- im Inneren des Würfels (100-2)3=941192 Würfel ohne grüne Seitenflächen.
Im Dreieck ABC sei CD die Winkelhalbierende des Innenwinkels bei C und E der Schnittpunkt der Parallelen zu CD durch B mit der Verlängerung von AC über C hinaus.Zeige, dass das Dreieck BCE immer gleichschenklig ist.
Lösung (von Manuel Mai, Leipzig):
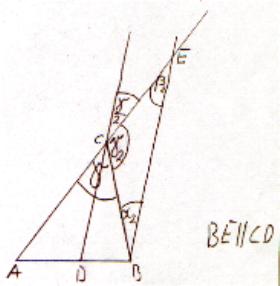
Im Folgenden bezeichnet w(XYZ) die Größe des Winkel mit Scheitel Y und Schenkeln XY und YZ.
Um zu zeigen, dass BCE ein gleichschenkliges Dreieck ist, muss man beweisen, dass zwei Innenwinkel gleich groß sind.
Wegen der Parallelität von BE und CD gilt aber einerseits w(DCB)=w(CBE) als Wechselwinkel und andererseits w(ACD)=w(CEB) als Stufenwinkel. Schließlich ist drittens w(ACD)=w(DCB), da nach Voraussetzung CD die Winkelhalbierende ist. Also gilt w(CBE)=w(CEB) und das Dreieck BCE ist wie behauptet gleichschenklig.
Ermittle die kleinste (echt) achtstellige natürliche Zahl z, für die folgendes gilt:(1) Alle Ziffern der Dezimaldarstellung sind verschieden.
(2) z ist durch 36 teilbar.
Lösung (von Manuel Mai, Leipzig):
Die kleinste achtstellige Zahl, bei der alle Ziffern der Dezimaldarstellung verschieden sind und die durch 36 teilbar ist, ist die Zahl 10237896.Da es keine kleinere achtstellige Zahl gibt außer 10xxxxxx, denn 01xxxxxx ist nicht möglich (die Zahl wäre siebenstellig), fing ich bei dieser Zahl an.
Ich dachte mir alle Zahlen der Form 10xxxxxx, die durch 9 und 4 teilbar sind ( Teilbarkeitsregel der 36), d.h. die Zahl musste gerade sein bzw. die letzten beiden Ziffern zusammengesehen durch 4 teilbar sein und ihre Quersumme musste durch 9 teilbar sein.
Die kleinste achtstellige Zahl, bei der die Ziffern der Dezimaldarstellung verschieden sind, ist die 10234567. Diese Zahl ist schon mal gar nicht durch 4 teilbar. Eine kleine durch 4 teilbare Zahl wäre die 10234568, diese ist aber nicht durch 9 teilbar, die Quersumme ergibt 29, damit die Zahl auch durch 9 teilbar ist könnte die Quersumme 36 ergeben.
Die ersten 4 Ziffern (1023) behielt ich, um eine kleine Zahl zu erhalten. Die Quersumme von 1023 ist 6, so müssten die restlichen 4 Ziffern eine Quersumme von 30 haben. 4567 hat eine Quersumme von 22, d.h. 8 zu wenig. 6789 hat eine Quersumme von 30, perfekt! Nun musste ich die Ziffern so anordnen, dass die letzen beiden Ziffern zusammengesehen durch 4 teilbar sind und trotzdem als erstes in der Anordung eine Ziffer, so klein wie möglich stehen sollte. So kam ich auf 7896.
Jetzt stimmte die Teilbarkeit mit 9 und mit 4, es war die kleinste durch 36 teilbare achtstellige Zahl mit unterschiedlichen Ziffern der Dezimaldarstellung.
Drei Kaufleute wollten einen Berg Goldstücke untereinander aufteilen, so dass der erste die Hälfte, der zweite ein Drittel und der dritte ein Sechstel der Gesamtzahl erhält.Zunächst hatte sich jeder einen Teil der Goldstücke genommen, so wie es ihm richtig erschien. Als alle Goldstücke verteilt waren, merkten sie, dass der dritte zu wenig abbekommen hatte. Deshalb legte jeder von ihnen etwas von den genommenen Goldstücken zurück; der erste die Hälfte der von ihm genommenen Goldstücke, der zweite ein Drittel und der dritte ein Sechstel. Diese Goldstücke verteilten sie zu gleichen Teilen untereinander, wonach jeder den ihm zustehenden Teil bekommen hatte.
Wieviele Goldstücke lagen am Anfang auf dem Tisch und wie wurden sie verteilt und umverteilt?
Lösung:
Wir lösen die Aufgabe mit einem Variablenansatz: Wenn der erste zunächst A Goldstücke, der zweite B Goldstücke und der dritte C Goldstücke genommen hat, so ergibt sich folgende Bilanz
Erster Zweiter Dritter Summe zuerst genommen A B C G = A + B + C
(Gesamtsumme)zurück gelegt - A/2 - B/3 - C/6 R = A/2 + B/3 + C/6
(Rückgabesumme)zweite Verteilung + R/3 + R/3 + R/3 Bilanz G/2 = A/2 + R/3 G/3 = 2/3*B + R/3 G/6 = 5/6*C + R/3 Aus der Bilanz erhalten wir
A = G - 2/3*R
B = G/2 - R/2
C = G/5 - 2/5*Rund somit
G = A + B + C = 17/10*G - 47/30*R, d.h. R = 21/47*G
Die Gesamtzahl G der Goldstücke war also durch 47 teilbar und es gilt
A = G - 2/3*R = 33/47*G
B = G/2 - R/2= 13/47*G
C = G/5 - 2/5*R = 1/47*GBei der ersten Verteilung ist der Dritte also wirklich schlecht davon gekommen; er hat nur 1/47 der Gesamtmenge Goldes abbekommen. Das müssen aber wenigstens 6 Goldstücke gewesen sein, denn sonst hätte er ja nicht 1/6 zurücklegen können. Also waren anfangs 6*47=282 Goldstücke (oder ein ganzzahliges Vielfaches davon) vorhanden. Diese Summe wurde wie folgt aufgeteilt:
Erster Zweiter Dritter zuerst genommen A=33/47*G=198 B=13/47*G=78 C=1/47*G=6 zurückgelegt -(A/2=99) -(B/3=26) -(C/6=1) zweite Verteilung +42 +42 +42 Bilanz 198-99+42=141=G/2 78-26+42=G/3 6-1+42=G/6
Sind alle schweren Fische freundlich zu Kindern ? Gib eine wasserdichte Begründung Deiner Aussage !
- Kein einziger Haifisch zweifelt daran, dass er gut bewaffnet ist.
- Ein Fisch, der nicht Walzer tanzen kann, verdient Mitleid.
- Kein einziger Fisch fühlt sich sicher bewaffnet, wenn er nicht mindestens drei Reihen von Zähnen hat.
- Alle Fische mit Ausnahme der Haifische sind freundlich zu Kindern.
- Schwere Fische können nicht Walzer tanzen.
- Fische mit mindestens drei Reihen von Zähnen verdienen kein Mitleid.
Lösung (von Carolin Schwarz, Leipzig):
(4): Alle Fische mit Ausnahme der Haifische sind freundlich zu Kindern. Da müssen wir also nur herausfinden, ob der Haifisch ein schwerer Fisch ist.(1): Kein Haifisch zweifelt, dass er gut bewaffnet ist.
(3): Kein einziger Fisch ist sicher bewaffnet, wenn er nicht mindestens drei Reihen von Zähnen hat. Also hat der Haifisch mindestens drei Reihen von Zähnen.
(6): Fische mit mindestens drei Reihen von Zähnen verdienen kein Mitleid. Also verdienen Haifische kein Mitleid.
(5): Schwere Fische können nicht Walzer tanzen.
(2): Ein Fisch, der nicht Walzer tanzen kann, verdient Mitleid. Also verdienen schwere Fische Mitleid. Also kann ein schwerer Fisch kein Haifisch sein, denn der verdient ja kein Mitleid, weil er gut bewaffnet ist.
Also sind alle schweren Fische freundlich zu Kindern, weil ja nur die Haifische nicht freundlich zu Kindern sind.
43_1_5_ ist eine siebenstellige Zahl, in der drei Ziffern fehlen. Untersuche, wie viele solche Zahlen es gibt, die durch 75 teilbar sind.
Lösung (nach Niels Kirstein, Leipzig):
Weil 75=3*25 ist, muss die zu bestimmende Zahl durch 3 und durch 25 teilbar sein. Wegen der Teilbarkeit durch 25 muss die Zahl auf 50 enden. Da jede Zahl, die auf 50 endet, durch 25 teilbar ist, muss nur noch die Teilbarkeit durch 3 gesichert werden. Bezeichnen wir die noch nicht bekannten Ziffern mit a und b, ao lautet die gesuchte Zahl 43a1b50.Eine Zahl ist genau dann durch 3 teilbar, wenn es ihre Quersumme ist. Die Quersumme der Zahl 43a1b50 beträgt gerade a+b+13. Genau die folgenden Kombinationen von a und b ergeben durch drei teilbare Quersummen:
a b Zahl der Paare 1,4,7 1,4,7 3*3=9 2,5,8 0,3,6,9 3*4=12 0,3,6,9 2,5,8 4*3=12 Zusammen gibt es also genau 9+12+12=33 siebenstellige Zahlen mit den geforderten Eigenschaften. Die kleinste ist 4301250, die größte 4391850.
Die Mathe-AG bietet zur Aufbesserung der AG-Kasse für das Schulfest ein Würfelspiel nach folgenden Regeln an:Es werden drei Würfeln gleichzeitig geworfen. Jeder Spieler darf auf eine der Zahlen 1, 2, 3, 4, 5, 6 setzen. Erscheint sie einmal, zweimal oder gar dreimal beim Würfeln, dann erhält er 2, 3 oder sogar 4 DM ausgezahlt. Anderenfalls geht der Spieler leer aus. Der Spieleinsatz beträgt 1 DM.
Untersuche, ob die Mathe-AG bei reger Spielbeteiligung eher Gewinn oder eher Verlust machen wird. Wie groß ist der zu erwartende Gewinn bzw. Verlust im Verhältnis zur Summe der Einsätze ?
Lösung (nach Carolin Schwarz, Leipzig):
Wir ermitteln zuerst, wie viele Ergebnisse es geben kann, wenn man mit drei Würfeln würfelt. Da auf jedem Würfel unabhängig von den anderen jede der Zahlen 1...6 stehen kann, gibt es insgesamt 6*6*6=216 verschiedene Ergebnisse und jedes von ihnen tritt mit derselben Wahrscheinlichkeit auf.Nun setzen wir auf die 6 (jede andere Zahl führt zum selben Ergebnis) und schauen, in wie vielen Fällen wir dabei einen Einer, Zweier oder gar Dreier haben werden.
Einer ergeben sich, wenn auf dem ersten Würfel eine 6 steht und auf dem zweiten und dritten je eine 1...5. Es gibt 25 solche Würfelkombinationen und ebenso viele, wenn die 6 auf dem zweiten und wenn sie auf dem dritten Wüfel steht. In 3*5*5=75 Fällen hätte ich also einen Einer.
Zweier entstehen, wenn auf zwei der Würfel eine 6 erscheint und auf dem letzten eine 1...5. Die Sechsen können auf den Würfeln 1 und 2, 1 und 3 oder 2 und 3 sein. Es gibt also 3*5=15 Fälle, wo ich einen Zweier gehabt hätte.
Einen Dreier gibt es unter den 216 Fällen genau einmal.
Wenn ich alle 216 Möglichkeiten durchspiele, so beträgt mein Einsatz 216 * 1 DM = 216 DM, der Gewinn
75 * 2 DM + 15 * 3 DM + 1 * 4 DM = 199 DM
Der Mathe-AG bleiben also noch ein paar Mark übrig. Der Gewinnanteil beträgt 17/216, also etwa 7.9 %.
Drei Männer sollen sich 21 gleich große Fässer Wein teilen, von denen 7 voll, 7 halbvoll und 7 leer sind. Kann man es so einrichten, dass jeder dieselbe Menge Wein und dieselbe Anzahl Fässer bekommt ?Carolin Schwarz, Leipzig, hat sogar zwei Lösungen gefunden:
Wir verwenden folgende Bezeichnungen:
v = volles Fass Wein h = halbvolles Fass Wein l = leeres Fass Wein 1. Lösung:
die erste Person bekommt 2v 3h 3l die zweite Person bekommt 2v 3h 3l die dritte Person bekommt 3v 1h 3l 2. Lösung:
die erste Person bekommt 3v 1h 3l die zweite Person bekommt 3v 1h 3l die dritte Person bekommt 1v 5h 1l In beiden Lösungen sind alle Fässer verteilt worden und jede Person hat 7 Fässer und 3.5 Fass Wein bekommen.
Anton, Bertram und Chris wollen einen Sack Weizen teilen. Leider haben die drei kein Maß zur Verfügung. Anton teilt den Weizen in drei seiner Meinung nach gleich große Haufen; aber die anderen beiden sind es nicht zufrieden. Bertram sagt: "Ja, wenn wir nur zwei wären, dann wäre es einfach: Ich teile und der andere sucht sich aus und alle wären es zufrieden."Mache einen Vorschlag, wie die drei Bauern ihren Weizen teilen können, so dass alle drei zufrieden sind.
Lösung von Carolin Schwarz, Leipzig:
Anton teilt den Weizen in zwei seiner Meinung nach gleich große Haufen. Bertram sucht sich einen der beiden Haufen aus. Anton und Bertram teilen ihre Haufen in drei ihrer Meinung nach gleichgroße Haufen. Chris sucht sich von jedem einen Haufen aus, so hat jeder seiner Meinung nach wenigstens 1/3 (= 2/6) des Weizens.Chris kann sich jetzt nicht beschweren, dass er weniger als ein Drittel hätte , weil er sich ja von Anton und Bertram jeweils den größten Haufen hätte aussuchen können.
Bertram kann sich jetzt nicht beschweren, dass er weniger als ein Drittel hätte, weil er sich ja von den von Anton geteilten Haufen den größeren Haufen hätte aussuchen können und er hat ja seinen Haufen in drei seiner Meinung nach gleich große Haufen geteilt.
Anton kann sich jetzt nicht beschweren, dass er weniger als ein Drittel hätte, weil er ja am Anfang den Weizen in zwei seiner Meinung nach gleich große Haufen geteilt hat und er hat ja seinen Haufen in drei seiner Meinung nach gleich große Haufen geteilt.